Contents

  1. Introduction
  2. Structure
  3. Add Operation

  4. Delete Operation

  5. LL class design
  6. Two Pointers

Introduction

In this lecture, we will turn our attention to another Data structure called Linked List. This is a sequential structure where each node know the address of it successor.

As illustrated in the previous figure, the structure of a linked list is based on a single node. Those nodes are linked using pointers (or reference) to the next node.

There are two types of linked lists according the representation of the node:

  1. Singly Linked Lists: Where each node knoes only the address of its successor.

  2. Doubly linked Lists: A node knows his successor and predecessor.

The objective of this chapter is

  • Understand this Data structure.
  • Code some basic operations such as insertion and deletion.
  • Analyse the complexity of those operations.
  • Introduce the advanced technique of the two pointers to solve some intermediate problems.

Data Structure

We will start by the basic structure (Singly Linked List). The declaration of a single node is given as:

  • A value (for now we could restraint ourselves to a int)
  • A pointer (the blue arrow) to the next element.

Hence we could encode this structure in order to store the information of such a node:

// Definition of a singly linked list
struct SinglyListNode {
    int val;
    SinglyListNode *next;

    //Constructor (this is how we will construct each node)
    SinglyListNode(int x) : val(x), next(nullptr) {}
};

In order to represent the list and similar the concept of an array, we will manage the list just by its head which refers to the first element.

The first remark is that compared to an array, we lost the ability to access each element in a constant time \(\mathcal{O}(1)\). For example, if we want to access the fifth element we must traverse all the previous ones. Hence accessing an element has a linear complexity \(\mathcal{O}(N)\).

Une question qu’on doit se poser est pourqu’oi on utilise une telle structure avec un tel inconvénient. La réponse réside dans les deux opérations de ajout et de suppression.

Hence a question arises, is that why we will sacrifice the efficiency of accessing elements. The answer is on the following advantages:

  1. A dynamic structure ( we are not constraint by a capacity)
  2. The insertion and suppression are much efficient.

Add Operation

Now we will try to code the first basic operation which is to add an node just after and node prev.

A single advice in coding data structure is to always draw a sketch representing your operations in the memory.

Ading at a given index

  1. Construct a node curr with the current value.
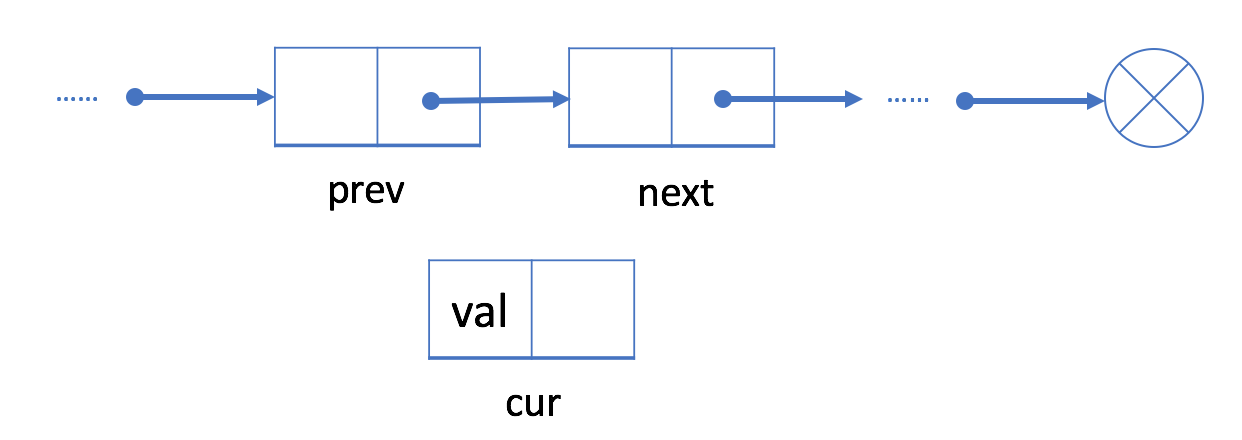
  1. Link its successor to the successor of prev.
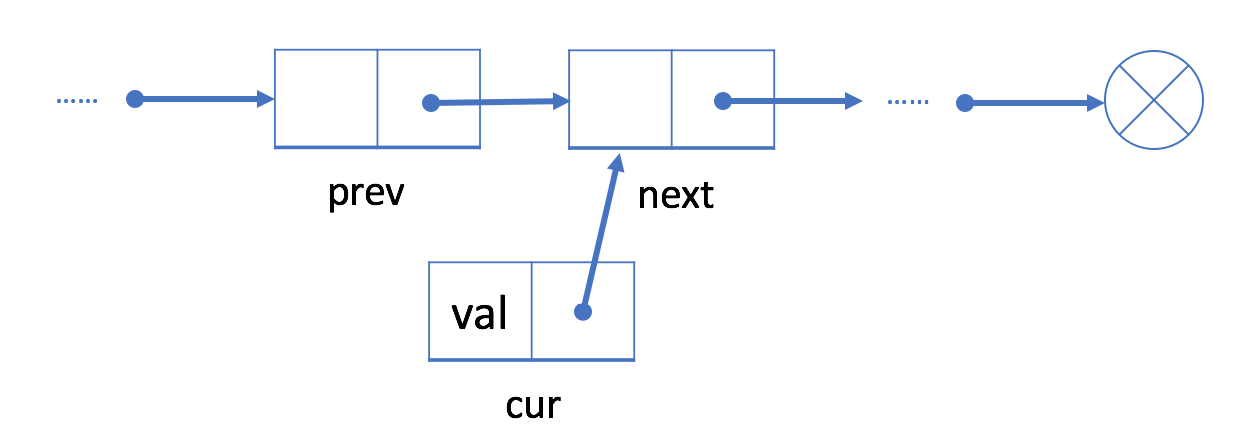
  1. Link the successor of prev to the current node.

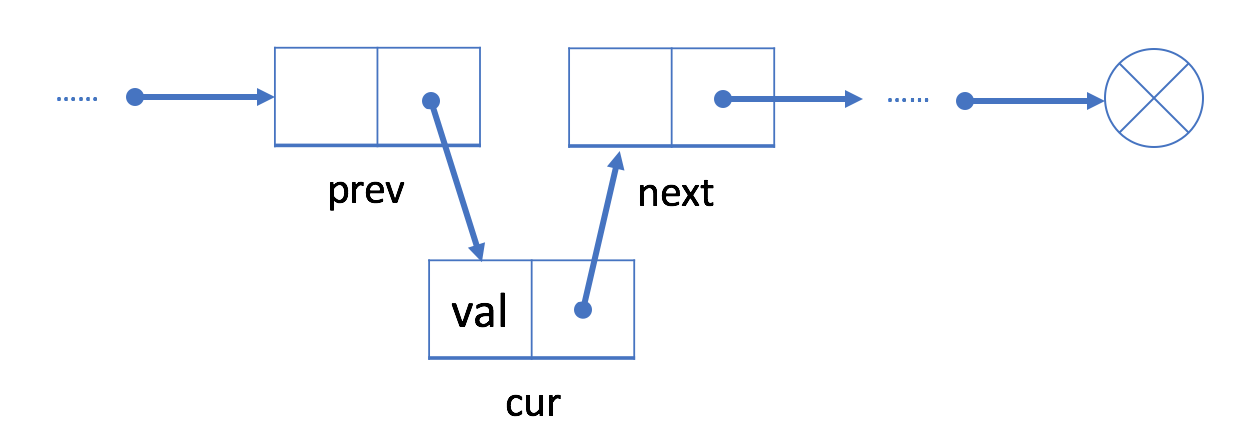
As illustrated in the previous scheme, this operations could be done in a constant time \(\mathcal{O}(1)\) without any constraint on the capacity.

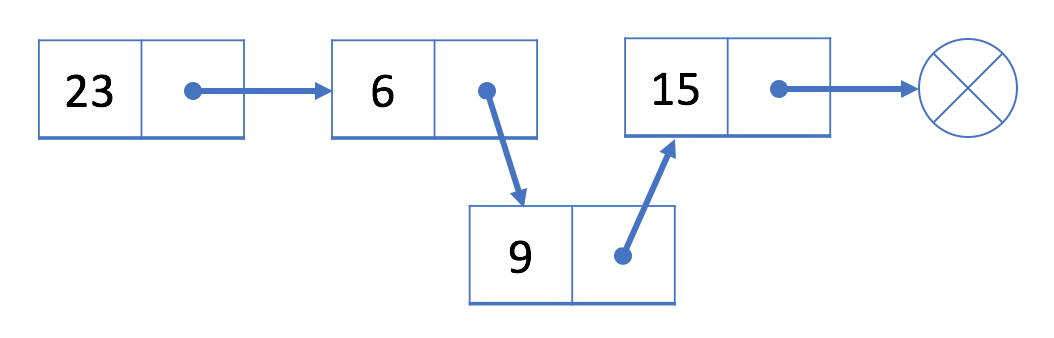
Example:

Lets consider the following Linked list

We want to insert the value \(9\) after \(6\).

We must then construct a node with value \(9\), link the \(9\) to \(15\). And then link the \(6\) to the value of \(9\).

Adding at the Beginning

The insertion at the begenning is a little different since we must change head itself.

  1. Construct the currentn node curr.
  2. Link the successor of curr to head.
  3. Update the head to curr.

Let’s illustrate the mecanism by adding \(9\) to the start of the list.

  1. Create the node curr with value \(9\) and link it to \(23\)
  1. Update the head to the node \(9\).

Delete Operation

Now we focus on deleting a node curr in the linked list.

  1. Find the predecessor of curr.
  1. Link prev and next.

If current lives in the heap don’t forget to free its space with delete.

We could analyze the complexity of this operation:

  1. We already have the pointers next and curr.
  2. But in order to access prev, we must travese the linked list

Hence the complexity is \(\mathcal{O}(N)\) for a Singly linked list.

Example:

Let’s consider the list

  • We want to delete the node \(6\).
  • Traverse the list in order to find the predessor of \(6\) which is \(23\).
  • Link \(23\) (prev) and \(15\) (next).

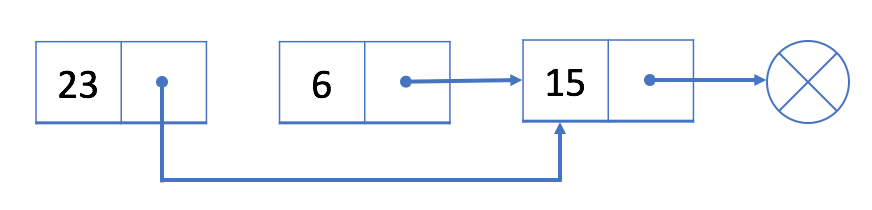
Same as the insertin, the deletion of an item must take custom care is the node we want to delete is the head.

In order to delte head, all we have to do it to push it to the next element:

  1. Let’s consider the deletion of the first element:
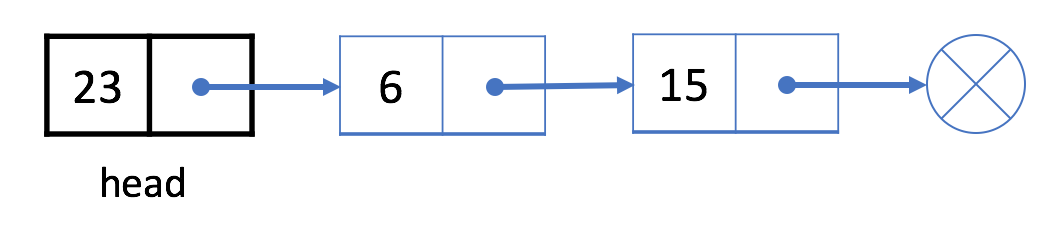
  1. Now \(6\) is the new head:

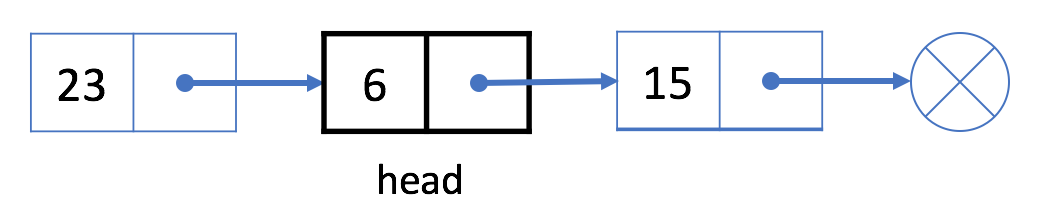
Réfléchir a la question de suppression du élément.

LL class design

Now we could implement the class (or structure) Linked List with the following operations:

In the singly_linked_list.zip, you’ll find a project with class LinkedList with the following members:

  • LinkedList : Constructor of the linked list.
  • size() : return its size.
  • int get(int index): return a pointer to the ith element if there is such an element otherwize \(-1\).
  • void addAtHead(int val) Add a note at the head.
  • void addAtTail(int val): add a node val at the end of the list.
  • void addAtIndex(int index, int val): add a val in a given index.
  • void deleteAtIndex(int index) : delete the node at a given index.
  • operator<< : to print the list.

Two pointers (Advanced)

Detect cycle

We will consider the technique of two pointers which uses (as the name suggests) two pointers to solve some problems efficietly.

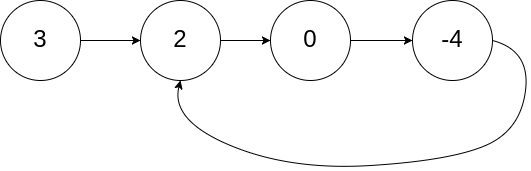
Let’s consider the problem of detecting cycles in a linked list.

Given the head of a list, determine is it has a cycle.

For example the following list \(\left(3,2, 0 , -4\right)\) has a cycle.

Here is another example with onlly two nodes:

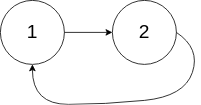
We could solve this problem by storing all the addresses in a map but this will lead to higher space complexity.

We will apply the two pointer to solve this problem in a faster way without the use of any additional datastructure.

Lets imagine tow runner in that list the first runner is faster and the secod one is slower

  1. If the list doesn’t have a cycle the faster runner will finish (attend nullptr) before the slower one.

  2. Now let’s imagine what will happen if the list has a cycle. Inevitably the faster runner will catch up the slower.

Hence the strategy is to take two pointer one slower advances by only one hop, and the other faster hopes two times.

Try to complete this function in the project detect_cycles.zip .

bool has_cycle(SinglyLinkedNode *head)